curl
(Q206310)
differential operator describing the rotation at a point in a 3D vector field
differential operator describing the rotation at a point in a 3D vector field
Language:
Current Data About
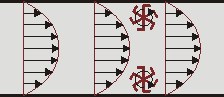
curl
| (P18) |
|
||||||||||||||||||
| (P279) |
(Q1058681)
(Q7917838) |
||||||||||||||||||
| (P1343) |
(Q109490582)
|
||||||||||||||||||
| (P1889) |
(Q9322940)
|
||||||||||||||||||
| (P2534) |
\nabla \times \boldsymbol{F} = \lim_{V \to 0} \frac{1}{V} \oint\limits_S \boldsymbol{e}_{\mathrm{n}} \times \boldsymbol{F} \, \mathrm{d} A
(\nabla \times \boldsymbol{F})_i = \sum_j \sum_k \varepsilon_{i j k} \frac{\partial F_k}{\partial x_j}
\nabla \times \boldsymbol{F} = \begin{pmatrix} \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \\ \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \\ \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \end{pmatrix} |
||||||||||||||||||
| (P5555) |
Curl.svg
|
||||||||||||||||||
| (P6104) |
(Q8487137)
|
||||||||||||||||||
| (P7235) |
\nabla \times \boldsymbol{F}
\boldsymbol{F}
S
\boldsymbol{e}_{\mathrm{n}}
A
V
\oint\limits_S \ldots \, \mathrm{d} A
\times
\varepsilon_{i j k}
|
other details
| aliases |
rotation curl of vector-valued function |
| description | differential operator describing the rotation at a point in a 3D vector field |
External Links